Morphology-Aware Graph Reinforcement Learning for Tensegrity Robot Locomotion

Abstract

Tensegrity robots combine rigid rods and elastic cables, offering high resilience and deployability but posing major challenges for locomotion control due to their underactuated and highly coupled dynamics. This paper introduces a morphology-aware reinforcement learning framework that integrates a graph neural network (GNN) into the Soft Actor-Critic (SAC) algorithm. By representing the robot’s physical topology as a graph, the proposed GNN-based policy captures coupling among components, enabling faster and more stable learning than conventional multilayer perceptron (MLP) policies. The method is validated on a physical 3-bar tensegrity robot across three locomotion primitives, including straight-line tracking and bidirectional turning. It shows superior sample efficiency, robustness to noise and stiffness variations, and improved trajectory accuracy. Notably, the learned policies transfer directly from simulation to hardware without fine-tuning, achieving stable real-world locomotion. These results demonstrate the advantages of incorporating structural priors into reinforcement learning for tensegrity robot control.

Motivation

Tensegrity robots maintain stability through a global balance of tension: every rod and cable contributes to the overall equilibrium. This intrinsic tensional coupling means that even a local actuation affects the entire structure, making their dynamics strongly interdependent and difficult to model with traditional independent-joint representations.

At the same time, this network of tensile and compressive elements naturally forms a graph. Such a structural property makes tensegrity systems particularly suitable for graph-based learning architectures.

Therefore, this work adopts a morphology-aware policy using a Graph Neural Network (GNN) that mirrors the robot’s physical topology. By aligning the control policy with the robot’s inherent graph structure, the agent can learn coordinated behaviors that respect the underlying physics of tension and coupling.

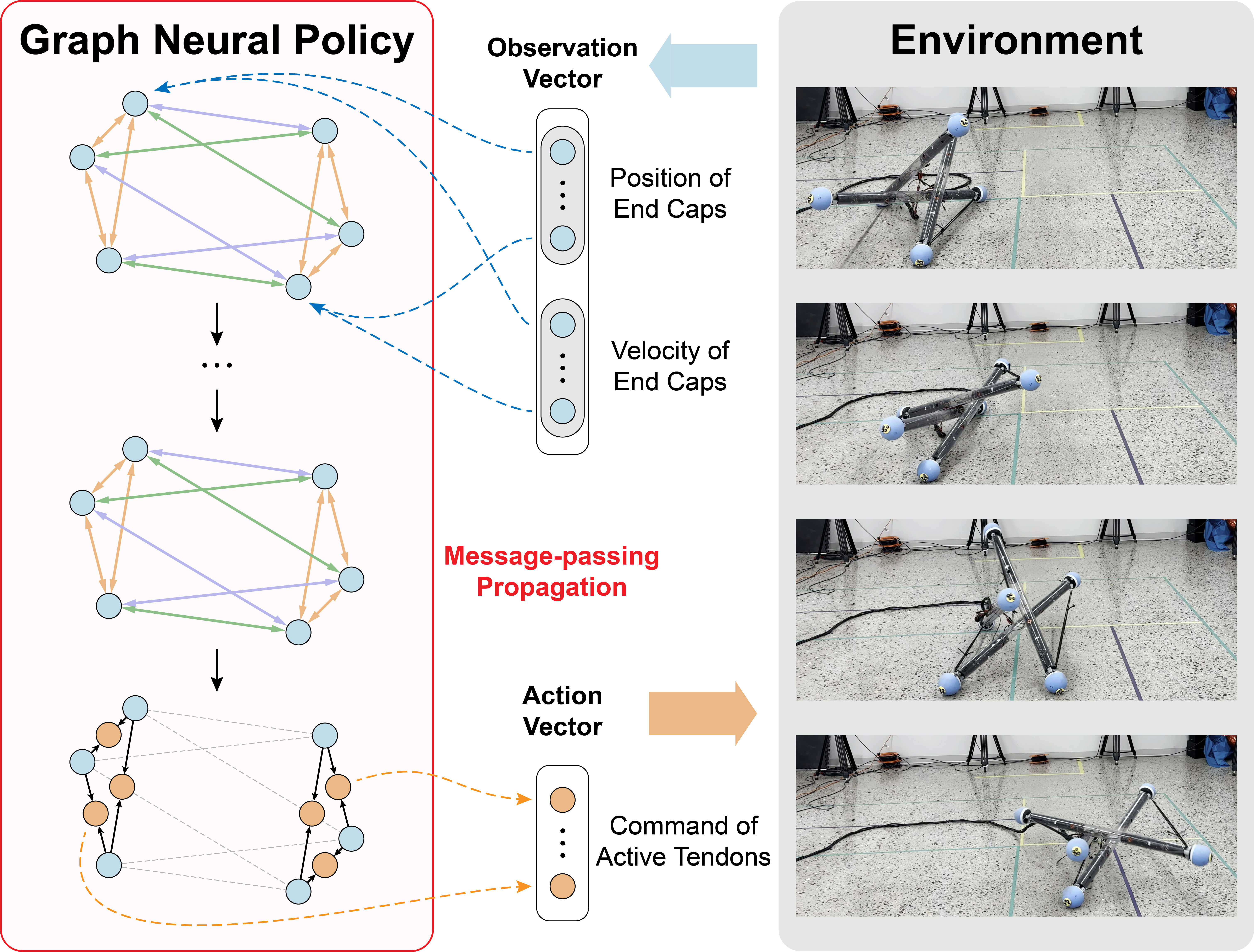Figure 1: Morphology-aware graph reinforcement learning for tensegrity locomotion. The robot’s states (end-cap positions and velocities) are encoded as node features in a graph-based policy, which propagates information along the robot’s structural connections. The network outputs tendon length commands to actuate the tensegrity robot to roll forward in physical experiments.

Methodology

• Graph Construction. The physical topology of the 3-bar tensegrity robot is modelled as a directed graph $G=(V,E)$, where each node corresponds to a rod end-cap, and edges represent mechanical connections (rigid rods, passive tendons, active tendons) allowing message passing between connected parts. Each node has features (e.g., 3D position, velocity of that end-cap, global task command broadcast), each edge has features encoding relative distance and edge type. The GNN encoder applies multiple layers of message passing over this graph to allow components to share structural information.

• GNN-based SAC (G-SAC). The GNN serves as the actor network within SAC. The observation encoding maps the raw robot state into node/edge features; the GNN encoder extracts a high‐level representation capturing structural coupling; the actor head outputs tendon length commands (actuation). The entire system is trained via the SAC algorithm on tracking and turning tasks.

• Training Formulation. The reward is formulated to support locomotion primitives: straight-line tracking, clockwise and counterclockwise in-place turning. The performance is compared with MLP-based SAC and other RL baselines.

Figure 2: Overview of the proposed morphology-aware GNN-SAC framework for tensegrity robot locomotion. The Soft Actor-Critic (SAC) algorithm integrates a graph neural network (GNN)-based policy that encodes the robot’s topology via message passing among end-cap nodes. The actor generates tendon length commands based on structured observations, enabling morphology-aware learning in both simulation and real-world environments.

Experimental Results

• RL Locomotion in Real World. The GNN-based policies trained for tensegrity locomotion are deployed to the real world with zero-shot transfer. The videos show motion primitives in the real world:

  • Straight-line Tracking
  • In-place Turning (Counter Clockwise)
  • In-place Turning (Clockwise)

• Benchmark of Learning Performance. GNN-based policies achieve higher sample efficiency and final rewards than standard MLP-based baselines.

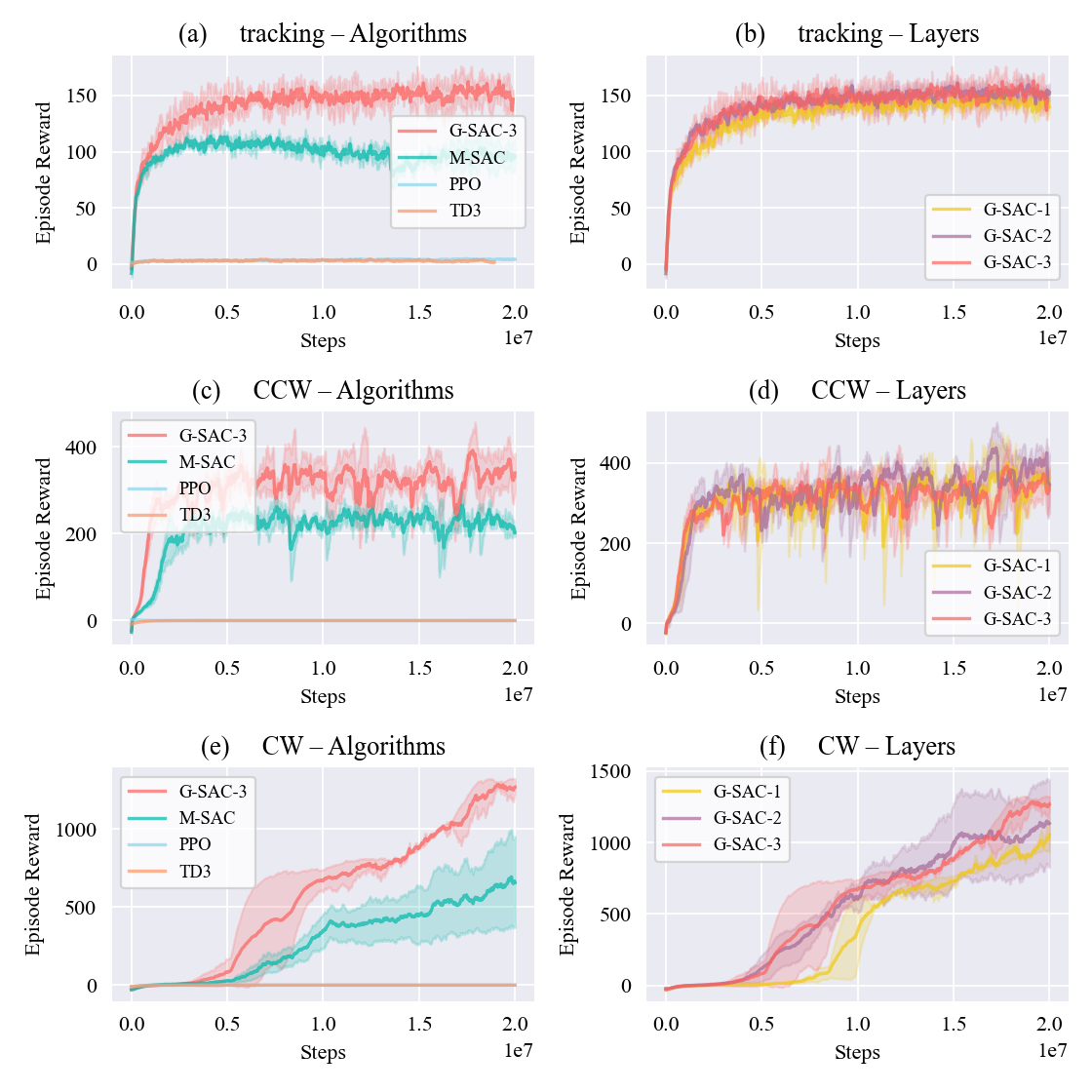  Figure 3: Benchmark of learning performance across algorithms and network depths. The proposed GNN-SAC consistently outperforms MLP-based SAC (M-SAC), PPO, and TD3 in terms of training reward and sample efficiency for all three locomotion primitives. Subplots (a,c,e) compare algorithms, while (b,d,f) analyze the effect of GNN encoder depth, showing improved performance with multi-layer message passing.

  The GNN-based policies also demonstrate improved directional accuracy and robustness in motion primitives.

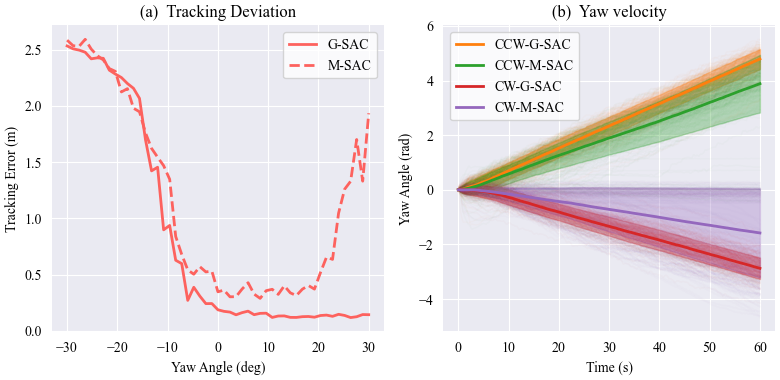  Figure 4: Simulation evaluation of learned motion primitives between Graph-based SAC (G-SAC) and MLP-based SAC (M-SAC): (a) Straight-line tracking error for different waypoint yaw angles; (b) Yaw rate and stability in bidirectional turning tasks.

• Robustness Evaluation. Three perturbations are introduced to evaluate robustness under real-world–like uncertainties:

  • Cross-tendon stiffness: varied from 30–1200 N/m (nominal 450~N/m) to capture material and assembly variations.

  • State estimation noise: Gaussian noise $\mathcal{N}(0, \sigma_n)$ with $\sigma_n \in [0, 0.25]$~m was added to end-cap positions to simulate degraded sensing.

  • Ground slope: inclinations from $0^{\circ}$ to $35^{\circ}$ were tested using policies trained on flat terrain.

  Across all perturbations and motion primitives, GNN-based policies consistently outperformed MLP-based baselines.

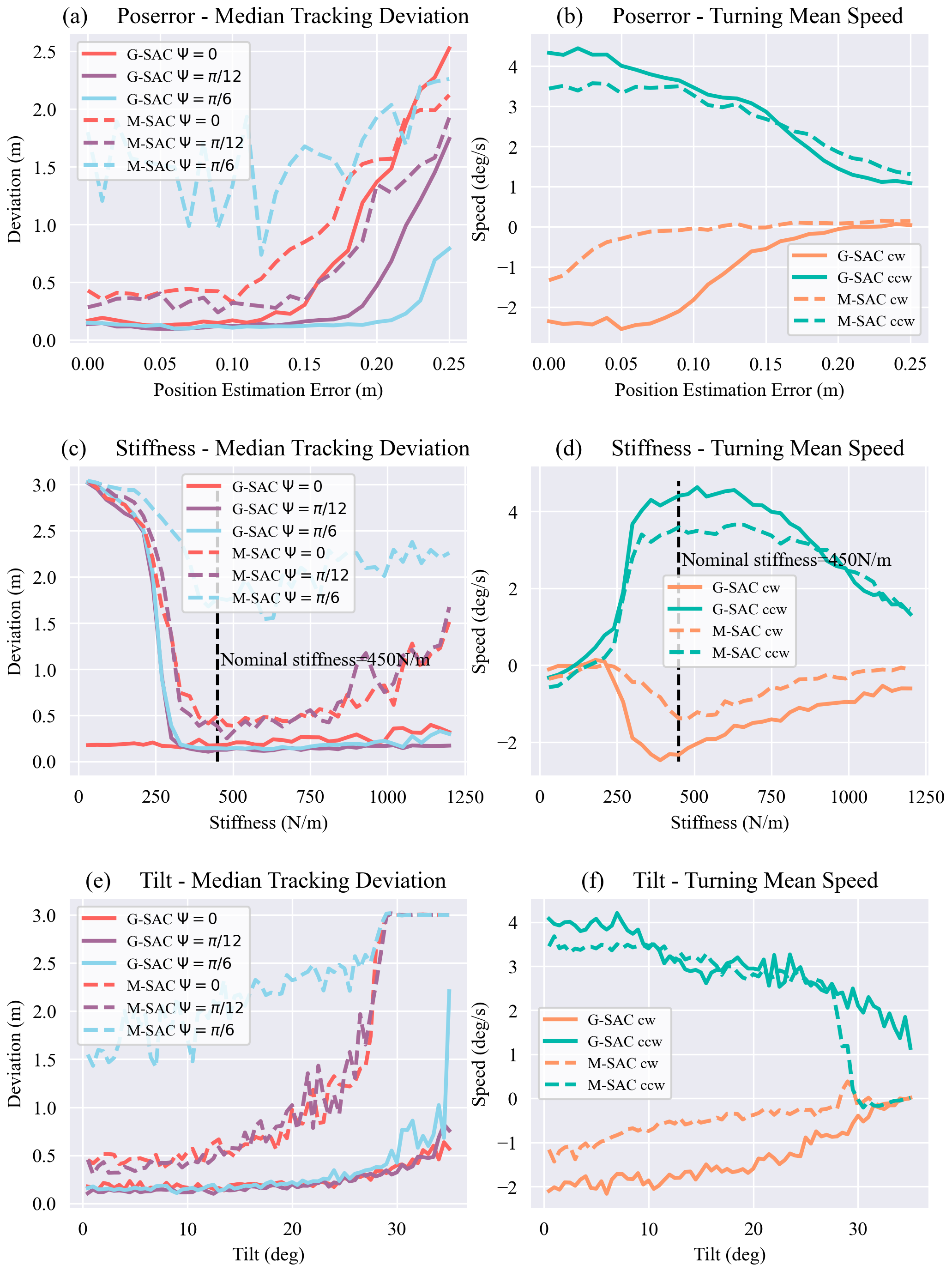  Figure 5: Robustness evaluation under model and environment perturbations. (a) (b) Cross-tendon stiffness variation, (c) (d) Observation noise, (e) (f) Ground slope.